[每日算法]过河卒

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

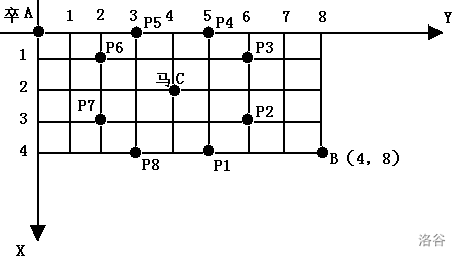
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

样例#1	输出#1
6 6 3 3	6

说明/提示

对于100% 的数据，，1 ≤n,m≤20，0≤ 马的坐标≤20。

题解

很明显这是个动态规划问题。状态转移方程为a【i】【j】=a【i-1】【j】+a【i】【j-1】。通过分析，发现要到达棋盘上的一个点，只能从左边或上面过来。所以，根据加法原理，到达某一点的路径数目，就等于到达其相邻的上点和左点的路径数目之和，因此我们可以使用逐列（或逐行）递推的方法来求出从起点到终点的路径数目。障碍点（马的控制点）也完全适用，只要将到达该店的路径数目设置为0即可。

源代码

#include<iostream>
#include <cmath>

using namespace std;

int main()
{
    int Bx, By, Hx, Hy;              //分别为B点坐标与马的位置
    int i, j;
    long long numbers[21][21];       //numbers[i][j]代表从A点到点(i,j)的线路条数
    bool horse[21][21];              //确定是不是马的势力范围

    //获取B点的坐标与马的坐标
    cin >> Bx >> By >> Hx >> Hy;
    //先全部位置标记为false，路径条数初始化为0
    for (i = 0;i <= Bx;i++)
    {
        for (j = 0;j <= By;j++)
        {
            horse[i][j] = false;
            numbers[i][j] = 0;
        }
    }

    //马的势力范围标记为true,最多有8个其他位置
    horse[Hx][Hy] = true;
    if (Hx + 2 <= Bx && Hy + 1 <= By) horse[Hx + 2][Hy + 1] = true;
    if (Hx + 1 <= Bx && Hy + 2 <= By) horse[Hx + 1][Hy + 2] = true;
    if (Hx - 1 >= 0 && Hy + 2 <= By) horse[Hx - 1][Hy + 2] = true;
    if (Hx - 2 >= 0 && Hy + 1 <= By) horse[Hx - 2][Hy + 1] = true;
    if (Hx - 2 >= 0 && Hy - 1 >= 0) horse[Hx - 2][Hy - 1] = true;
    if (Hx - 1 >= 0 && Hy - 2 >= 0) horse[Hx - 1][Hy - 2] = true;
    if (Hx + 1 <= Bx && Hy - 2 >= 0) horse[Hx + 1][Hy - 2] = true;
    if (Hx + 2 <= Bx && Hy - 1 >= 0) horse[Hx + 2][Hy - 1] = true;

    //动态规划求解
    for (i = 0; i <= Bx; i++) 
    {
        for (j = 0; j <= By; j++) 
        {   //如果有马就不能走
            if (horse[i][j] == 0)
            {   //A点设置为1
                if (i == 0 && j == 0)
                    numbers[i][j] = 1;
                //第一行的其他点只能从该点左边过来
                else if (i == 0 && j > 0)
                    numbers[i][j] = max(numbers[i][j],numbers[i][j - 1]);
                //第一列的其他点只能从该点的上一个点到达
                else if (i > 0 && j == 0)
                    numbers[i][j] = max(numbers[i][j],numbers[i - 1][j]);
                //其他点可从上方和右方到达
                else
                    numbers[i][j] = max(numbers[i][j],numbers[i - 1][j] + numbers[i][j - 1]);
            }
        }
    }

    cout << numbers[Bx][By];
    return 0;
}